Vitorino Ramos, David M.S. Rodrigues, Jorge Louçã, “Spatio-Temporal Dynamics on Co-Evolved Stigmergy“, in European Conference on Complex Systems, ECCS’11, Vienna, Austria, Sept. 12-16 2011.
Ever tried to solve a problem where its own problem statement is changing constantly? Have a look on our approach:
Abstract: Research over hard NP-complete Combinatorial Optimization Problems (COP’s) has been focused in recent years, on several robust bio-inspired meta-heuristics, like those involving Evolutionary Computation (EC) algorithmic paradigms. One particularly successful well-know meta-heuristic approach is based on Swarm Intelligence (SI), i.e., the self-organized stigmergic-based property of a complex system whereby the collective behaviors of (unsophisticated) entities interacting locally with their environment cause coherent functional global patterns to emerge. This line of research recognized as Ant Colony Optimization (ACO), uses a set of stochastic cooperating ant-like agents to find good solutions, using self-organized stigmergy as an indirect form of communication mediated by artificial pheromone, whereas agents deposit pheromone-signs on the edges of the problem-related graph complex network, encompassing a family of successful algorithmic variations such as: Ant Systems (AS), Ant Colony Systems (ACS), Max-Min Ant Systems (Max–Min AS) and Ant-Q.
Albeit being extremely successful these algorithms mostly rely on positive feedback’s, causing excessive algorithmic exploitation over the entire combinatorial search space. This is particularly evident over well known benchmarks as the symmetrical Traveling Salesman Problem (TSP). Being these systems comprised of a large number of frequently similar components or events, the principal challenge is to understand how the components interact to produce a complex pattern feasible solution (in our case study, an optimal robust solution for hard NP-complete dynamic TSP-like combinatorial problems). A suitable approach is to first understand the role of two basic modes of interaction among the components of Self-Organizing (SO) Swarm-Intelligent-like systems: positive and negative feedback. While positive feedback promotes a snowballing auto-catalytic effect (e.g. trail pheromone upgrading over the network; exploitation of the search space), taking an initial change in a system and reinforcing that change in the same direction as the initial deviation (self-enhancement and amplification) allowing the entire colony to exploit some past and present solutions (environmental dynamic memory), negative feedback such as pheromone evaporation ensure that the overall learning system does not stables or freezes itself on a particular configuration (innovation; search space exploration). Although this kind of (global) delayed negative feedback is important (evaporation), for the many reasons given above, there is however strong assumptions that other negative feedbacks are present in nature, which could also play a role over increased convergence, namely implicit-like negative feedbacks. As in the case for positive feedbacks, there is no reason not to explore increasingly distributed and adaptive algorithmic variations where negative feedback is also imposed implicitly (not only explicitly) over each network edge, while the entire colony seeks for better answers in due time.
In order to overcome this hard search space exploitation-exploration compromise, our present algorithmic approach follows the route of very recent biological findings showing that forager ants lay attractive trail pheromones to guide nest mates to food, but where, the effectiveness of foraging networks were improved if pheromones could also be used to repel foragers from unrewarding routes. Increasing empirical evidences for such a negative trail pheromone exists, deployed by Pharaoh’s ants (Monomorium pharaonis) as a ‘no entry‘ signal to mark unrewarding foraging paths. The new algorithm comprises a second order approach to Swarm Intelligence, as pheromone-based no entry-signals cues, were introduced, co-evolving with the standard pheromone distributions (collective cognitive maps) in the aforementioned known algorithms.
To exhaustively test his adaptive response and robustness, we have recurred to different dynamic optimization problems. Medium-size and large-sized dynamic TSP problems were created. Settings and parameters such as, environmental upgrade frequencies, landscape changing or network topological speed severity, and type of dynamic were tested. Results prove that the present co-evolved two-type pheromone swarm intelligence algorithm is able to quickly track increasing swift changes on the dynamic TSP complex network, compared to standard algorithms.
Keywords: Self-Organization, Stigmergy, Co-Evolution, Swarm Intelligence, Dynamic Optimization, Foraging, Cooperative Learning, Combinatorial Optimization problems, Dynamical Symmetrical Traveling Salesman Problems (TSP).
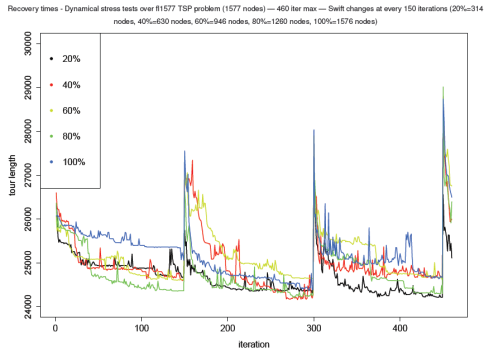
Fig. – Recovery times over several dynamical stress tests at the fl1577 TSP problem (1577 node graph) – 460 iter max – Swift changes at every 150 iterations (20% = 314 nodes, 40% = 630 nodes, 60% = 946 nodes, 80% = 1260 nodes, 100% = 1576 nodes). [click to enlarge]




